The simulations used in Lab Books are all based on a simple core program that stores location information for each displayed particle and updates that location for each unit of time (called a time slice).
 As each particle
moves, two random numbers are drawn: one is used to update the x-axis
position, the other to update the y-axis position. The random numbers
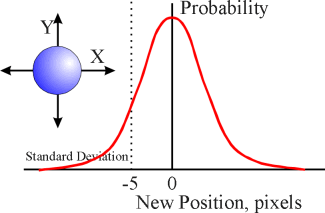
themselves are produced from an algorithm that calculates its output according
to a bell-shaped (Gaussian) curve. The peak probability of this Gaussian
distribution is set at zero, with decreasing probability of seeing either
a positive or negative value further and further from zero. For the
simulations used here, the Gaussian distribution for single particles and
water molecules has a standard deviation (SD) of 5 units, while the Gaussian
distribution for the movement of larger ion/water assemblies is much more
tightly clustered around the mean, having an SD of 2 units. As with all
Gaussian distributions, +/- 1 SD accounts for about two-thirds of all the
values; +/- 3 SD includes 99% of all possible values.
As each particle
moves, two random numbers are drawn: one is used to update the x-axis
position, the other to update the y-axis position. The random numbers
themselves are produced from an algorithm that calculates its output according
to a bell-shaped (Gaussian) curve. The peak probability of this Gaussian
distribution is set at zero, with decreasing probability of seeing either
a positive or negative value further and further from zero. For the
simulations used here, the Gaussian distribution for single particles and
water molecules has a standard deviation (SD) of 5 units, while the Gaussian
distribution for the movement of larger ion/water assemblies is much more
tightly clustered around the mean, having an SD of 2 units. As with all
Gaussian distributions, +/- 1 SD accounts for about two-thirds of all the
values; +/- 3 SD includes 99% of all possible values.
This random walk scheme approximates Brownian (diffusion) movement actually observed in a solution. Each molecule in a real solution, however, is vibrating and continuously colliding and interacting with its neighbors, but these events occur on a time scale faster than we can observe and simulate. During a period equivalent to our time slice, the "net" movement simulated is the average of a large number of such collisions and interactions. The average of a large number of such random events is well described by the bell-shaped Gaussian curve used for our calculations. Also, solute molecules in solution are transiently associated with water molecules, but these associations change more rapidly than we can simulate. Thus, we illustrate solvated solute assemblies in our osmosis simulations as if they contained the same water molecules all the time. Clearly, they don't but our approximation is not unreasonable.
Before the position of each particle is updated, a few checks are done. If the new position would lie beyond the borders of the box, then the particle "bounces". If the new position is on the other side of a membrane barrier, then a new random number is drawn to see if the particle can cross the membrane. These probabilities are determined by a formula (called the constant field equation) that relates permeation through a membrane to its voltage and intrinsic permeability. Using this approach, our membrane transport simulations reproduce well the actual movement of ions and other molecules across a real membrane. An ion or other solute that fails to permeate "bounces" off the membrane just as it did off the wall.
In the various Nernst simulations the only effect of voltage is in determining the membrane-crossing probability; voltage exerts no influence on the movement of individual particles in the free solution. Likewise, in the osmosis simulations the membrane is freely permeable to water molecules but not to the larger complexes of water and solute. Otherwise, the only force "driving" the various movements are the Gaussian random numbers in the x and y directions.
The programs themselves are written in the language Java. They make use of the concept of "object-oriented" programming by making each element in the simulation responsible for its own properties. Thus, each particle knows how to draw itself, stores its position and charge, and updates its position based on the constraints placed on its motion.